研究内容:本文采用分子动力学模拟方法研究了不同小分子自组装的结构差异。
背景分析
实验研究发现,黄芩苷与血根碱按照1:1的比例放入水溶剂环境中能自组装形成纳米团簇;β-甘草次酸自身在比例为DMSO:H2O的溶剂环境中也能自组装形成纳米团簇。为了研究它们最终自组装形成的结构特征以及整个自组装过程中分子间的主要驱动力,本文采用分子动力学(Molecular dynamics, MD)模拟方法对两个体系中小分子的自组装过程展开了研究。
方法速览
首先构建6 nm×6 nm×6 nm的模拟盒子,并分别随机填充20个黄芩苷、20个血根碱和40个β-甘草次酸分子,组成2个模拟体系。MD模拟采用Gromacs 2018.4程序[1],在恒温恒压以及周期性边界条件下进行。应用GAFF全原子力场,TIP3P水模型[2]。在MD模拟过程中,所有涉及氢键采用LINCS算法[3]进行约束,积分步长为2 fs。静电相互作用采用(Particle-mesh Ewald)PME方法[4]计算。非键相互作用截断值设为10 Å,每10步更新一次。采用V-rescale [5]温度耦合方法控制模拟温度为298.15 K,采用Parrinello-Rahman方法[6]控制压力为1 bar。首先,采用最陡下降法对四个体系进行能量最小化,以消除原子间过近的接触;然后,在298.15 K进行100 ps的NVT平衡模拟;最后,分别对2个不同体系分别进行100 ns的MD模拟,每10 ps保存一次构象,模拟结果可视化采用Gromacs内嵌程序和VMD完成。
结果分析
模拟收敛参数分析
均方根偏差(Root mean square deviation, RMSD)表示某一时刻的构象与目标构象所有原子偏差的加和,是衡量体系是否稳定的重要依据。图1a和b分别给出了Sanguinarine-Baicalin和Glycyrrhetinic acid 2个体系中小分子所有原子的RMSD值随模拟时间的变化。从图1a中可以看出,Sanguinarine-Baicalin体系的RMSD值在模拟过程中的波动相对较小,而Glycyrrhetinic acid的RMSD波动较大,二者在整个模拟过程中的平均值分别为3.024±0.103 nm和3.051±0.144 nm。整体来讲,Sanguinarine-Baicalin体系在模拟过程中RMSD的波动相对较小,表明这个体系在模拟过程中更加稳定。

图1 2个体系所有原子的RMSD(a和b)随模拟时间的变化
随着纳米粒子在自组装的进行,暴露在溶剂环境中的面积会逐渐减小,因此溶剂可及表面积(SASA)可以用来评价纳米粒子的紧密程度。图2a和b分别给出了2个体系在模拟过程中的溶剂可及表面积的相对变化,从整体上看,2个体系的SASA值在模拟过程中均出现了不同程度的降低,表明2个体系在模拟过程中均出现了不同程度的聚集现象。具体来讲,从图2中可以看出,2个体系的SASA值在模拟初始阶段都出现了非常明显的降低,随后减小速度放缓,并在40 ns后趋于稳定,2个体系的SASA平均值分别为69.940±4.864 nm2和92.328±4.126 nm2。由于两个体系中包含的分子不同,结构体积存在差异,不能横向对比,但两个体系中的SASA都明显降低并趋于稳定表明两个体系中的分子都能自组装形成更为紧密的纳米团簇,使其暴露在溶剂中的原子减少。
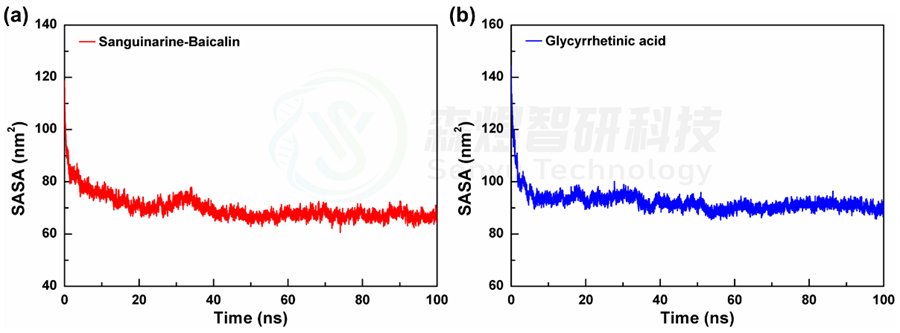
图2 2个体系溶剂可及表面积(a和b)随模拟时间的变化
聚类分析
为了研究模拟2个体系在模拟前后的构象变化以及自组装的结构紧密程度,本文采用Gromacs的cluster模块对四个体系中70-100 ns的模拟轨迹进行聚类分析,设置均方根偏差(Root mean square deviation, RMSD)截断值为1.2 nm。分别取体系最大簇的结构作为MD模拟的最终构象,如图3和4所示。从图3中可以看出,Sanguinarine-Baicalin体系自组装形成纤维状的纳米团簇结构。
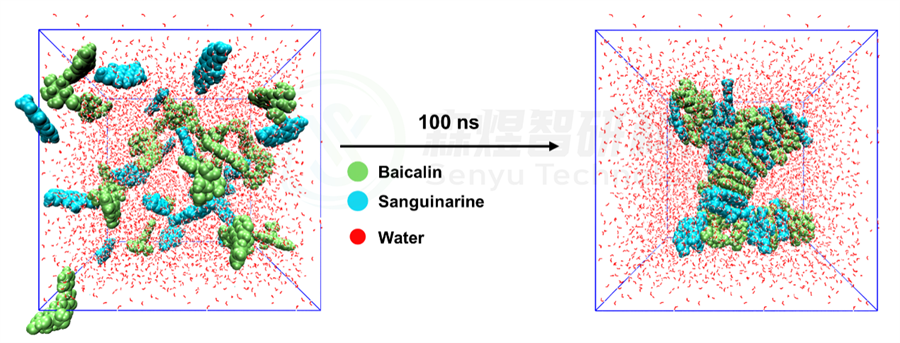
图3 Sanguinarine-Baicalin体系在模拟过程中的初末态结构变化
从图4中可以看出,经过100 ns的MD模拟之后,Glycyrrhetinic acid体系中所有小分子形成了比较稳定的,致密的类似球状的纳米团簇结构。
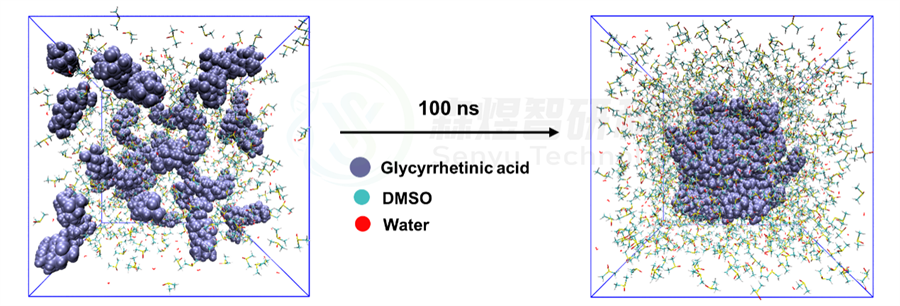
图4 Glycyrrhetinic acid体系在模拟过程中的初末态结构变化
随后,为了能更清楚的展现两个体系中小分子随着模拟进行不断自组装的动态过程,本研究对两个体系中的分子结构每间隔20 ns取一帧结构作为代表性构象进行绘图,如图6和图7所示,两个体系中的分子在分子间的相互作用下随着模拟的进行不短的聚集,最终形成具有一定形态的稳定纳米团簇结构。

图5 Sanguinarine-Baicalin体系在模拟过程中的结构随时间的变化

图6 Glycyrrhetinic acid体系在模拟过程中的结构随时间的变化
分子间相互作用分析
为了进一步研究体系自组装成纳米粒子过程中的驱动力,本文对MD模拟过程中的分子间的氢键数量进行了统计分析。如图7所示,从图中可以看出,在Glycyrrhetinic acid体系中,氢键作用相对较少,平均值为0.864±0.929个,而Sanguinarine-Baicalin体系中的氢键作用数量平均值为5.041±1.893个。整体来讲,Sanguinarine-Baicalin体系中的氢键数量比Glycyrrhetinic acid体系中明显更多,表明体系中分子间的相互作用更强,较多的氢键作用也可以使其组装的纳米粒子结构更加紧密。
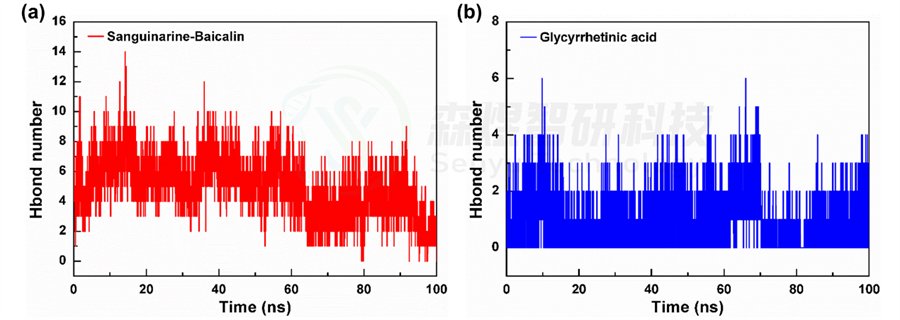
图7 Sanguinarine-Baicalin(a)和Glycyrrhetinic acid(b)体系中分子间的氢键数目随模拟时间的变化
随后,为了能更好的展现两个体系中分子间自组装的驱动力, 本文利用gmx_energy插件对两个体系中代表性分子间的相互作用能随模拟时间的变化进行了分析,结果如图8所示。其中Coul-SR代表静电能,主要作用类型为氢键或离子键等;LJ-SR代表范德华能,主要作用类型为各种共轭作用。在Sanguinarine-Baicalin体系中Sanguinarine和Baicalin分子间的Coul-SR平均值为-13.437±6.981 kJ/mol,LJ-SR平均值为-71.624±10.169 kJ/mol;在Glycyrrhetinic acid体系中,Glycyrrhetinic acid分子间的Coul-SR平均值为-2.350±6.798 kJ/mol,LJ-SR平均值为-64.286±8.683 kJ/mol。对比两个体系中自组装分子间的结合能可以发现,在Sanguinarine-Baicalin体系中Sanguinarine和Baicalin分子间的相互作用强于Glycyrrhetinic acid体系中Glycyrrhetinic acid分子间的相互作用,更强的相互作用能表明分子间更易自组装形成纳米团簇并且结构更加紧密。

图8 Sanguinarine-Baicalin(a)和Glycyrrhetinic acid(b)体系中分子间结合能随模拟时间的变化
分子间相互作用模式
通过前面分析不同分子体系的自组装过程中的相互作用能的强弱变化,发现Sanguinarine-Baicalin体系中分子间的相互作用力相对较强, Glycyrrhetinic acid体系中分子间的相互作用力相对较弱,因此为了深入研究不同结构所造成的的自组装差异,本文对MD模拟之后2个体系的构象进行了深入分析,如图9和图10所示。图9为Sanguinarine-Baicalin体系中分子间的相互作用示意图,从图9中可以看出,Sanguinarine分子和Baicalin分子主要通过分子中的大量的环状结构导致彼此间形成的Pi-Pi共轭作用促进其自组装,同时,Baicalin分子末端的羟基与Sanguinarine分子环上的氧原子间形成一组氢键作用,Baicalin分子内部的羟基与羰基氧原子间形成了分子内氢键作用(图9a)。Sanguinarine分子与Sanguinarine分子间主要是通过Pi-Pi共轭作用结合(图9b);Baicalin分子与Baicalin分子间促进其结合的主要有Pi-Pi共轭作用、分子间氢键和分子内氢键作用(图9c)。

图9 Sanguinarine-Baicalin体系中分子间的相互作用模式
图10为Glycyrrhetinic acid体系中分子间的相互作用示意图,从图10中可以看出,体系内的Glycyrrhetinic acid分子间主要通过分子中一个Glycyrrhetinic acid分子上的甲基与另一个分子上的六元环分子间形成的Pi-Sigma共轭作用促进其自组装,并且由于每个环上都连有甲基分子,导致分子间的空间位阻较大,Glycyrrhetinic acid分子之间没有形成明显的氢键作用。

图10 Glycyrrhetinic acid体系中分子间的相互作用模式
结论简述
本文采用MD方法模拟了Sanguinarine-Baicalin和Glycyrrhetinic acid两个体系组装成纳米结构的过程进行了研究。通过分析分子间相互作用力的变化,表明两个体系中的分子都能组装形成较稳定的纳米结构,Sanguinarine-Baicalin体系中主要的驱动力包括Pi-Pi共轭作用、分子间氢键和分子内氢键作用;Glycyrrhetinic acid体系中主要的驱动力为Pi-Sigma共轭作用。对两个体系最终组装形成的纳米团簇结构分析发现,Sanguinarine-Baicalin体系最终共组装形成纤维状的纳米结构,Glycyrrhetinic acid体系最终自组装形成类似球状的纳米团簇结构。
参考文献
[1] Van d S D , Lindahl E , Hess B , et al. GROMACS: Fast, flexible, and free. Journal of Computational Chemistry, 2005, 26(16):1701-1718.
[2] Jorgensen W L , Chandrasekhar J , Madura J D , et al. Comparison of simple potential functions for simulating liquid water. Journal of Chemical Physics, 1983, 79(2):926-935.
[3] Hess B , Bekker H , Berendsen H J C , et al. LINCS: A linear constraint solver for molecular simulations. Journal of Chemical Theory & Computation, 1997, 4(1):1463–1472.
[4] Darden T A , York D M , Pedersen L G . Particle mesh Ewald-an N.log(N) method for Ewald sums in large systems. The Journal of Chemical Physics, 1992, 98:10089-10092.
[5] Berendsen H J C , Postma J P M , Van Gunsteren W F , et al. Molecular dynamics with coupling to an external bath. Journal of Chemical Physics, 1984, 81(8):3684-3690.
[6] R Martonák, Laio A , Parrinello M . Predicting Crystal Structures: The Parrinello-Rahman Method Revisited. Physical Review Letters, 2003, 90(7):075503.
文献链接




