研究内容:本文采用分子动力学模拟方法研究了姜黄素和白藜芦醇与直链淀粉的分子识别
结构建模
V型直链淀粉(Amylose)由35个葡萄糖单位组成,葡萄糖单位间以α-糖苷键相连。直链淀粉结构通过GLYCAM网站构建,姜黄素(Curcumin)和白藜芦醇(Resveratrol)结构通过PubChem下载。三个分子的结构如图1所示。
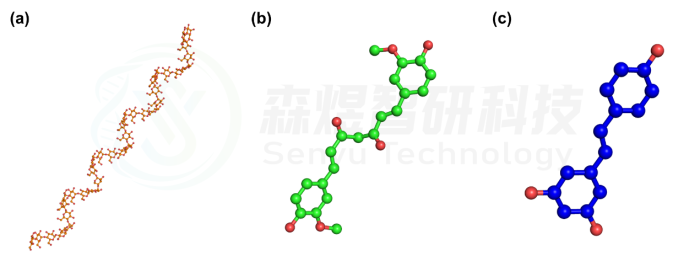
图1 Amylose三维结构(a);Curcumin三维结构(b);Resveratrol三维结构(c)
结果分析
小分子与支链淀粉复合物分子动力学模拟结果
对Curcumin和Resveratrol与Amylose复合物分别进行MD模拟,以观察两个小分子与支链淀粉的结合是否稳定及其相互作用机制。将Amylose-Curcumin和Amylose-Resveratrol复合物体系进行MD模拟后,分别提取模拟后的最终构象,如图2所示,经过100 ns模拟,Amylose-Curcumin和Amylose-Resveratrol复合物体系中两个小分子依然能稳定与Amylose结合,只是在模拟过程中螺旋状的Amylose分子发生了一定的空间构象改变。
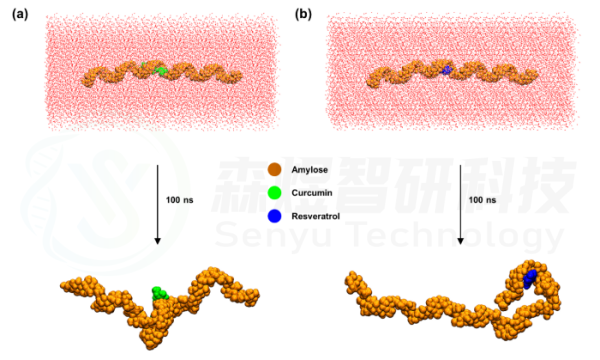
图2 Amylose-Curcumin和Amylose-Resveratrol复合物体系模拟前后空间构象
随后,为了更详细的观察两个小分子与支链淀粉复合物在整个模拟过程中的动态变化过程,我们对两个体系在模拟过程中复合物的构象进行了分析,每间隔20 ns截取一个稳定构象,Amylose-Curcumin结果如图3所示。在整个模拟过程中,尽管Amylose分子的空间构象有所改变,但是整个过程中Curcumin分子都与Amylose分子稳定的结合。
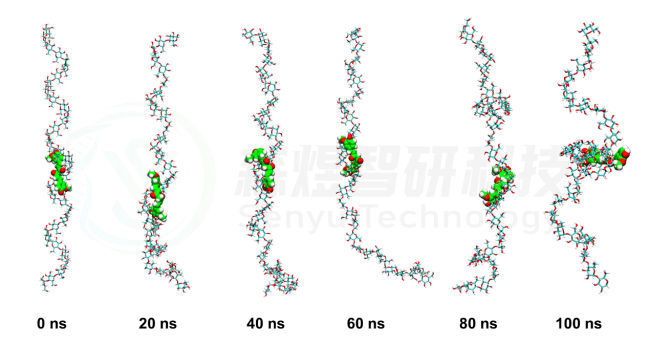
图3 Amylose-Curcumin复合物的构象随模拟时间的变化
Amylose-Resveratrol结果如图4所示。在整个模拟过程中,尽管Amylose分子的空间构象有所改变,但是整个过程中Resveratrol分子都与Amylose分子稳定的结合。
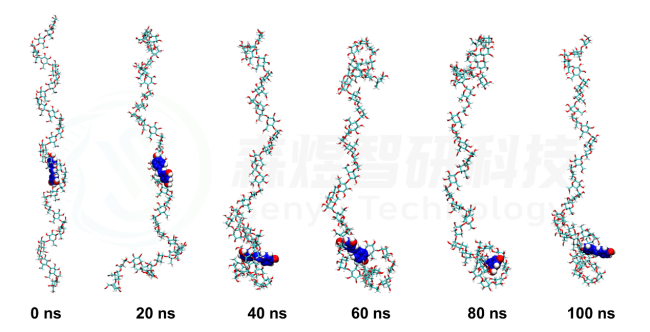
图4 Amylose-Resveratrol复合物的构象随模拟时间的变化
模拟收敛参数分析
均方根偏差(Root mean square deviation, RMSD)表示某一时刻的构象与目标构象所有原子偏差的加和,是衡量体系是否稳定的重要依据。图3a给出了两个复合体系中所有原子的RMSD值随模拟时间的变化,可以观察到两个体系的RMSD值在模拟过程中都存在一定幅度的波动,可能是因为直链淀粉分子两端在溶剂分子的影响下发生了一定的构象改变。两个体系的RMSD平均值分别为1.352±0.476 nm和1.638±0.308 nm,两个体系RMSD的波动幅度分别为35.21%和18.80%,两个体系整体的波动幅度都挺大,但如此大的波动幅度是否影响两个小分子与Amylose间的相互作用需进一步深入分析。
回转半径(Radius of Gyration, Rg)可以用来衡量分子整体结构的密实度,如果分子的空间结构很稳定,其Rg将保持一个相对稳定的值,Rg变化越大表明体系越膨胀。图3b给出了两个复合体系中所有原子的Rg值随模拟时间的变化,模拟初期,两个体系的Rg值小幅降低,随后在60 ns之前都趋于一个较为稳定状态,随后在70 ns左右,两个体系的Rg值都发生了一定程度的下降,此时两个体系中的Amylose分子构象发生了改变,结合前面的模拟前后构象对比分析,表明在模拟后期两个体系中的Amylose分子构象发生了折叠,但两个小分子依然稳定的结合在Amylose分子上。两个体系整个过程中Rg的平均值分别为2.828±0.445 nm和2.764±0.296 nm。
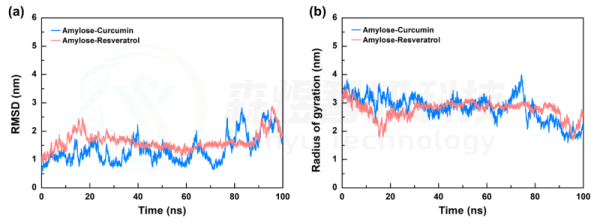
图5 Amylose-Curcumin和Amylose-Resveratrol复合物体系的RMSD和Rg值随模拟时间的变化
动力学模拟中复合物密度分析
随后,为了进一步分析两个复合物在模拟过程中的结合紧密程度,分别对两个体系中复合物,Amylose和两个小分子的密度沿盒子 z 轴的密度分布进行分析。从图4中可以看出,两个小分子在模拟过程中都是结合在Amylose分子中间的。从Amylose分子的密度分布可以发现,在Amylose-Curcumin体系中,Amylose分子最大密度更大,表明该体系中Amylose分子折叠得更厉害,同时Curcumin稳定结合在该位置;而在Amylose-Resveratrol体系中,mylose分子最大密度更小,表明该体系中Amylose分子结构更舒展,同时Resveratrol分子结合在密度最大位置旁边,单整个过程中Resveratrol也是一直稳定结合在Amylose分子上的。
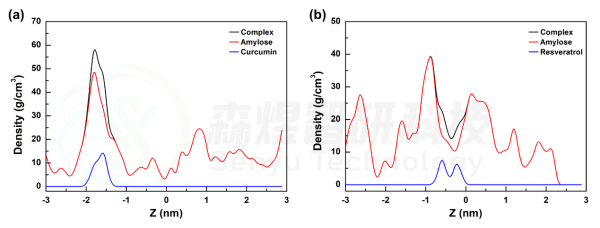
图6 Amylose-Curcumin(a)和Amylose-Resveratrol(b)复合物体系中各组分的密度分布
复合物与溶剂间氢键分析
当复合物置于溶剂盒子中时,其与溶剂分子间的氢键变化可以表征体系中复合物内小分子与Amylose分子间结合是否稳定,若Amylose分子空间构象发生明显折叠聚集,则其与溶剂水分子间的氢键会明显减少,反之则维持稳定;同样若小分子在模拟过程中从Amylose分子上游离,那小分子与溶剂分子间的氢键数会增加。两个体系中复合物、Amylose分子和小分子与溶剂水分子间的氢键数量随模拟时间的变化如图5所示。结果显示,在Amylose-Curcumin体系中,Amylose分子与水分子间的氢键较模拟初始时有一定减少,表明该体系中Amylose分子经过一定时间模拟后螺旋结构发生了变构折叠,而Curcumin分子与水分子间的氢键一直维持稳定,表明小分子与Amylose分子间一直稳定结合,并未出现游离。在Amylose-Resveratrol体系中,Amylose分子与水分子间的氢键在模拟过程中有一定减少,随后又增长回来,表明该体系中Amylose分子在模拟过程中发生过一定程度的变构折叠,但随着模拟的进行又舒展开来,Resveratrol分子与水分子间的氢键一直维持稳定,表明小分子与Amylose分子间一直稳定结合,并未出现游离。
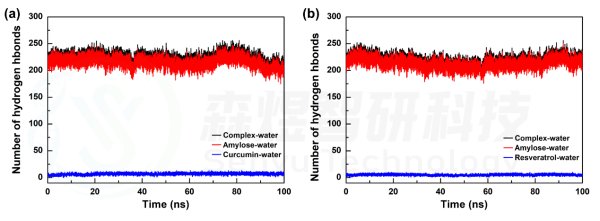
图7 Amylose-Curcumin(a)和Amylose-Resveratrol(b)复合物体系中各组分与水分子间的氢键随模拟时间的变化
分子间氢键和疏水作用分析
促进分子间结合的弱相互作用主要包括氢键作用、静电作用、疏水作用、π-π、π-sigma 和π-阳离子共轭作用,通常两个分子间的结合主要通过氢键作用和疏水相互作用作用驱动力。因此,本文对两个体系中Curcumin和Resveratrol分子与Amylose间的氢键作用和疏水作用随模拟时间的变化进行了分析,结果如图6所示。从图中可以发现,Curcumin分子与Amylose分子间的氢键作用较Resveratrol分子略强,两个体系中整个模拟过程中的氢键平均值分别为1.22和0.79。图6b为两个体系中Curcumin和Resveratrol分子与Amylose间疏水相互作用随模拟时间的变化,两个体系的平均值分别为2.46和1.99。两个体系中Curcumin分子与Amylose分子间的氢键作用的疏水作用都略强于Resveratrol分子,表明可能Curcumin分子与Amylose分子间的相互作用更强。
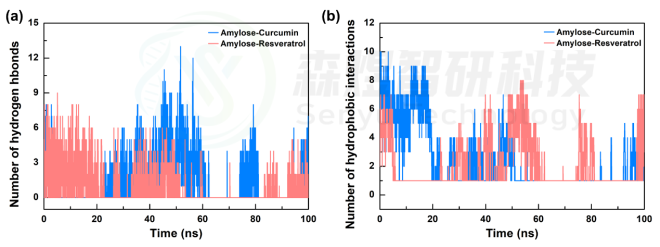
图8 Amylose-Curcumin和Amylose-Resveratrol复合物体系中小分子与Amylose间的氢键作用(a)和疏水作用(b)随模拟时间的变化
复合物SASA分析
溶剂可及表面积(Solvent accessible surface area, SASA)可以通过表征复合物体系在溶剂环境中可被溶剂接触的分子表面积来分析模拟过程中小分子和Amylose分子在溶剂条件下的结构体积变化,SASA值越大表明结构更松散,体积也更大,反之。在Amylose-Curcumin复合物体系中,Amylose分子的SASA值较初始状态时SASA值降低了约13%,表明该体系中Amylose分子经过一定时间模拟后螺旋结构发生了变构折叠,整体体积减小;而在Amylose-Resveratrol复合物体系中,虽然模拟过程中Amylose分子的SASA值有所下降,但末态相较于初态SASA值几乎没有下降,表明该体系中Amylose分子在模拟过程中发生过一定程度的变构折叠,但随着模拟的进行又舒展开来,最终Amylose分子体积无明显变化。进一步分析了两个体系中的小分子的SASA值,可以发现两个小分子的SASA值无明显减小,表明整个模拟过程中小分子的空间构象并未发生明显变化。从图7b中两个复合物的SASA值变化也可以看出,在Amylose-Curcumin复合物体系中,由于Amylose分子的变构折叠使整个复合物体系的SASA略有减小,而在Amylose-Resveratrol复合物体系中无明显变化。上述结果进一步表明,在Amylose-Curcumin复合物体系Amylose分子变构折叠,体积减小,同时Curcumin分子结合在Amylose分子变构折叠区域,可能进一步增强两个分子间的相互作用,而Amylose-Resveratrol复合物体系中Amylose分子仅发生小幅变化,并且Resveratrol分子也并未结合在该位置,因此它们间的相互作用可能与初始状态无明显变化。
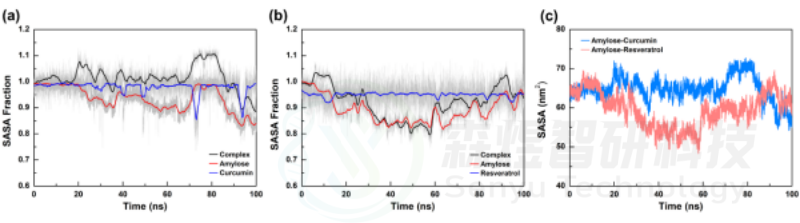
图9 Amylose-Curcumin和Amylose-Resveratrol复合物体系中SASA随模拟时间的变化(a:各组分的SASA比例随模拟时间的变化;b:两个复合物体系SASA值随模拟时间变化)
相互作用模式分析
图8给出了Curcumin分子和Resveratrol分子与Amylose分子间的结合模式,从图8a和b中可以看出,Curcumin分子结合在Amylose分子中17-25位葡萄糖分子形成的螺旋空腔中,Curcumin分子分别与17位葡萄糖分子上的O6、20位葡萄糖分子上的O6和25位葡萄糖分子上的O3间形成氢键作用,同时还与18、19、21、22和23位葡萄糖基间形成疏水相互作用,进一步促进两个分子间稳定结合。从图8b和c中可以看出,Resveratrol分子结合在Amylose分子中19-24位葡萄糖分子形成的螺旋空腔中,Resveratrol分子分别与22位葡萄糖分子上的O6和24位葡萄糖分子上的O2间形成氢键作用,同时还与19、20、21和23位葡萄糖基间形成疏水相互作用,进一步促进两个分子间稳定结合。
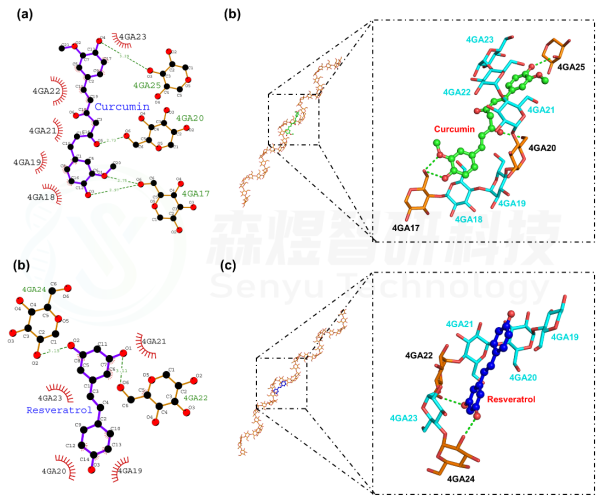
图10 Curcumin分子和Resveratrol分子与Amylose分子间的结合模式(a:Curcumin分子与Amylose分子间的2D结合模式,齿状糖基分子为疏水相互作用,绿色虚线为氢键作用;b:Curcumin分子与Amylose分子间的3D结合模式,Cyan色糖基为疏水基团,绿色虚线为氢键作用;c:Resveratrol分子与Amylose分子间的2D结合模式,齿状糖基分子为疏水相互作用,绿色虚线为氢键作用;d:Resveratrol分子与Amylose分子间的3D结合模式,Cyan色糖基为疏水基团,绿色虚线为氢键作用)
结论
本文采用MD模拟方法对Curcumin分子和Resveratrol分子与Amylose分子间的分子识别及其稳定性进行了对比分析,通过对比分析发现,两个小分子都能与Amylose分子间产生稳定的相互作用。进一步对比两个分子与Amylose分子间的氢键作用和疏水相互作用结果表明Curcumin分子与Amylose分子间的相互作用可能较Resveratrol分子更强。
参考文献
[1] Sanner M F. Python: a programming language for software integration and development. J. Mol. Graph. Model., 1999, 17(1): 57-61.
[2] Stewart J J. MOPAC: a semiempirical molecular orbital program. J. Comput. Aid. Mol. Des., 1990, 4(1): 1-105.
[3] Stewart J J P. Optimization of parameters for semiempirical methods. III. Extension of PM3 to Be, Mg, Zn, Ga, Ge, As, Se, Cd, In, Sn, Sb, Te, Hg, Tl, Pb, and Bi. John Wiley & Sons Inc., 1991.
[4] Maier J A, Martinez C, Kasavajhala K, et al. ff14SB: Improving the accuracy of protein side chain and backbone parameters from ff99SB. Journal of Chemical Theory and Computation, 2015, 11(8): 3696-3713.
[5] Van d S D , Lindahl E , Hess B , et al. GROMACS: Fast, flexible, and free. Journal of Computational Chemistry, 2005, 26(16):1701-1718.
[6] J. Comput. Chem. GLYCAM06: A generalizable biomolecular force field. Carbohydrates[J]. 2008.
[7] Jorgensen W L , Chandrasekhar J , Madura J D , et al. Comparison of simple potential functions for simulating liquid water. Journal of Chemical Physics, 1983, 79(2):926-935.
[8] Hess B , Bekker H , Berendsen H J C , et al. LINCS: A linear constraint solver for molecular simulations. Journal of Chemical Theory & Computation, 1997, 4(1):1463–1472.
[9] Darden T A , York D M , Pedersen L G . Particle mesh Ewald-an N.log(N) method for Ewald sums in large systems. The Journal of Chemical Physics, 1992, 98:10089-10092.
[10] Berendsen H J C , Postma J P M , Van Gunsteren W F , et al. Molecular dynamics with coupling to an external bath. Journal of Chemical Physics, 1984, 81(8):3684-3690.
[11] R Martonák, Laio A , Parrinello M . Predicting Crystal Structures: The Parrinello-Rahman Method Revisited. Physical Review Letters, 2003, 90(7):075503.



