1 蛋白结构建模
以产气荚膜梭菌α毒素蛋白三维结构(PDB代码为1CA1[1])作为模板,根据客户提供的产气荚膜梭菌α毒素蛋白(CPA)结构的完整序列,将其与1CA1蛋白序列比对,结果如图1所示,两个蛋白间的序列一致性为99.46%。随后,采用SWISS-MODEL程序[2]对CPA蛋白进行同源建模,从而获取可用于后续分子识别研究的CPA蛋白三维结构模型,建模得到的蛋白结构如图2a所示。

图1CPA蛋白与1CA1蛋白序列比对结果
用PROCHECK[3]程序对补全并优化后的蛋白模型进行了评价。Ramachandran plot用于阐述蛋白质或肽立体结构中肽键内α碳原子和羰基碳原子间的键旋转度对α碳原子和氮原子间的键的旋转度,主要用来指明蛋白质或肽类中氨基酸残基的允许和不允许的构象。Ramachandran plot主要分为三个区域,完全允许区(红色区域),允许区(黄色区域),不允许区(空白区域)。图2b给出了CPA蛋白的Ramachandran plot结果,位于完全允许区的氨基酸占比为91.8%,位于允许区的氨基酸占比为7.3%,总和超过了99%,没有氨基酸残基位于扭转角禁止区域,因此表明建模所得CPA蛋白所有氨基酸残基的二面角均在合理范围内,符合立体化学能量规则。
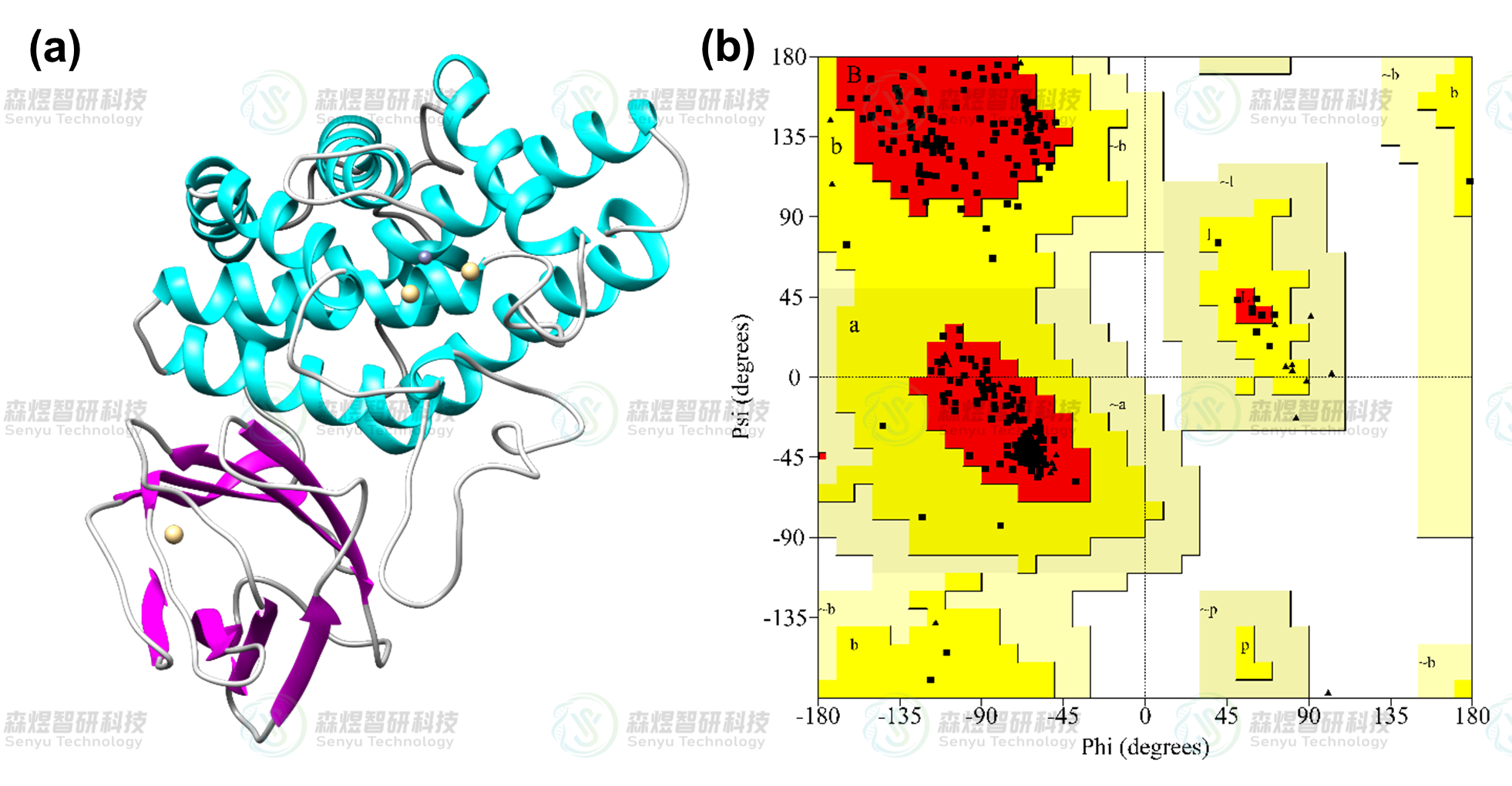
图2CPA蛋白结构(a)和CPA蛋白模型的Ramachandran Plot(b)
2 分子对接计算
2.1 受体结构准备
将同源建模得到的CPA蛋白作为初始结构用于后续的分子对接。初始结构用AutoDock Tools 1.5.6[4]进行处理,保存蛋白原有电荷,并生成pdbqt文件用于对接。
2.2 配体结构准备
杨梅黄酮(MYR)底物分子结构从PubChem数据库下载,使用MOPAC程序[5]优化分子结构并计算PM3原子电荷[6]用于后续分子对接,采用AutoDock Tools 1.5.6处理配体结构,生成pdbqt文件用于对接。
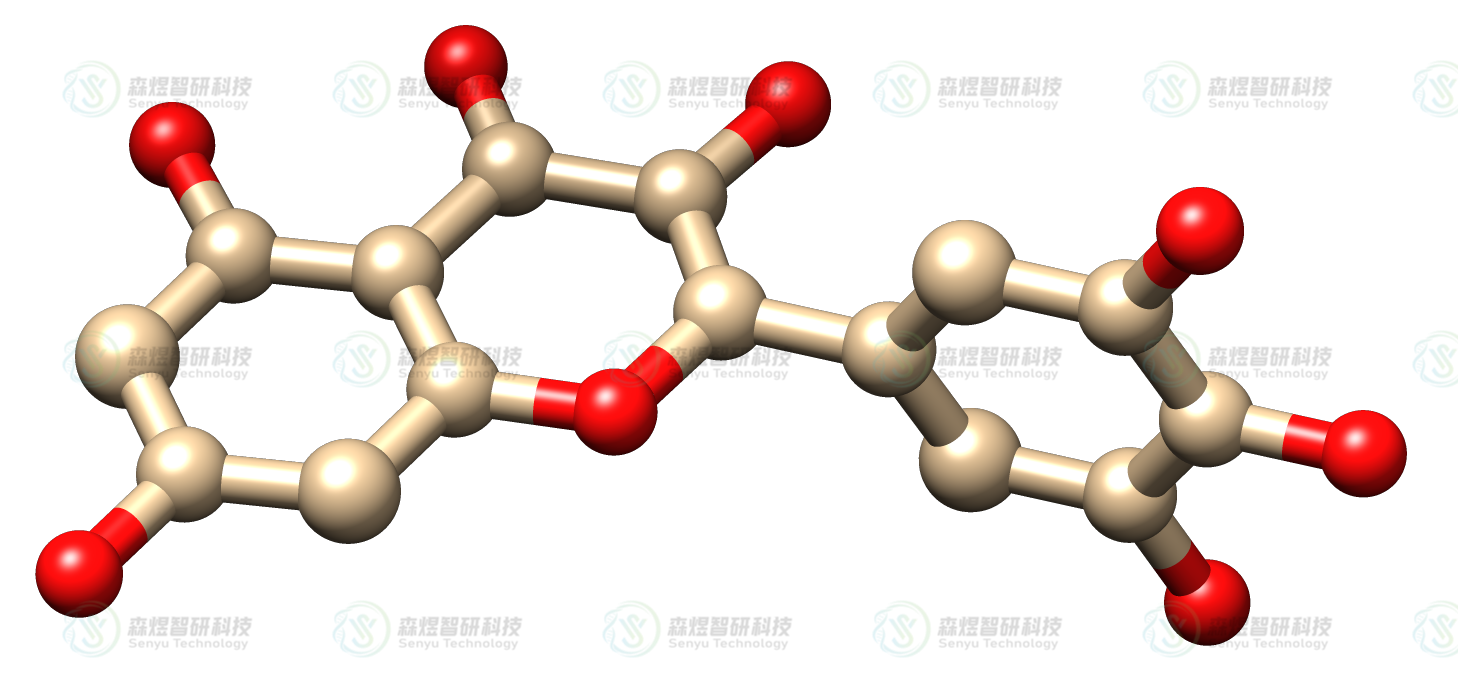
图3MYR分子的结构
2.3 分子对接方法
通过文献调研发现,分子MYR在CPA蛋白上的结合位点位于蛋白中几段α-Helix结构围成空腔上方,空腔底部存在一个Zn2+离子和两个Cd2+离子(如图4所示),有利于分子与CPA蛋白中的活性空腔结合,占据底物的结合位点,抑制该蛋白的活性。因此本文将MYR分子与蛋白的结合位点也定于此口袋,使其能竞争性抑制蛋白的活性。分子对接采用AutoDock 4.2.6软件包实现,对接盒子中心坐标设为(12.701,19.827,28.957),XYZ各方向的格点数设为60×60×60,对接次数设为100,其余参数采用默认值。
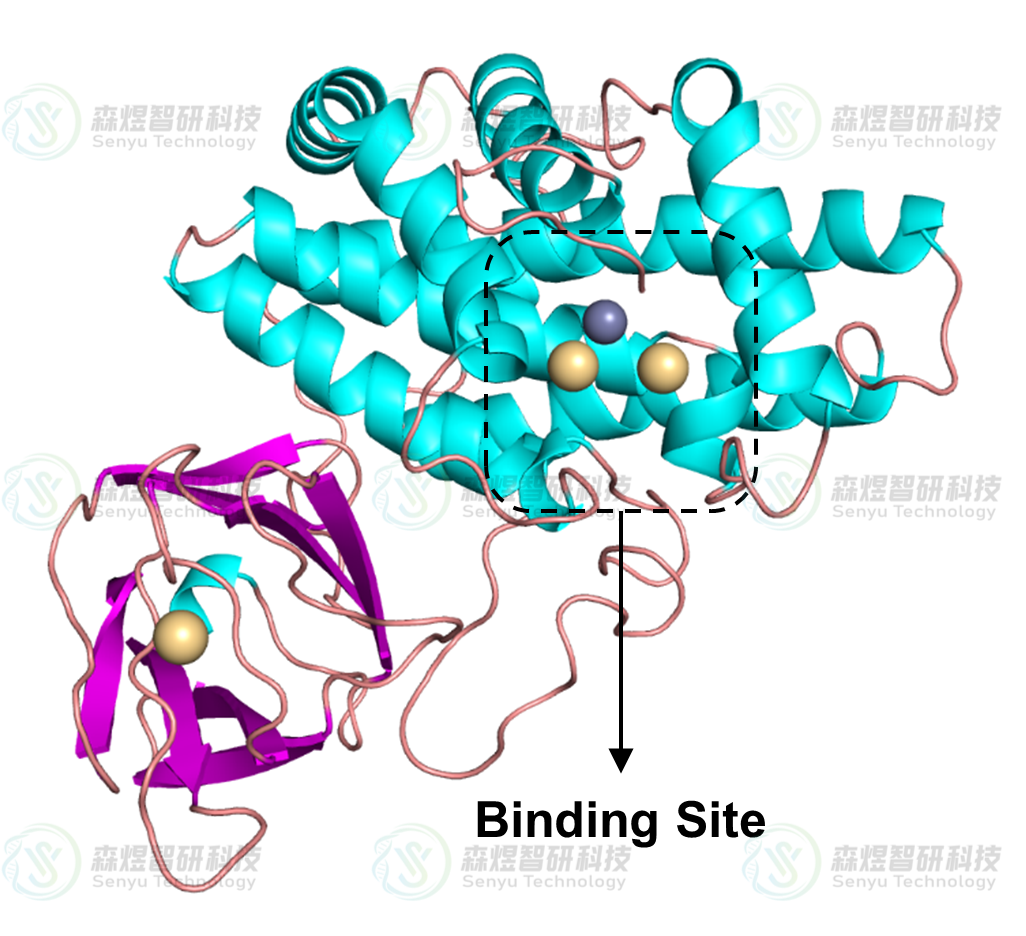
图4 CPA蛋白三维结构示意图,黑色虚线表示底物和蛋白结合位点。
2.4 对接结果优化
分子对接的结果在空间结构上可能存在不合理的原子接触,可以采用能量优化的方法对这些作用力进行释放,使其更趋于稳定结构。能量优化采用Amber14力场[7],优化过程分两步进行:先进行1000步的最陡下降法(Steepest Descent Method)优化,再用500步的共轭梯度法(Conjugate Gradient Method)对结构进行进一步优化,并将最终的结果作为后续分析的模型,最终得到的复合物结构如图5所示。
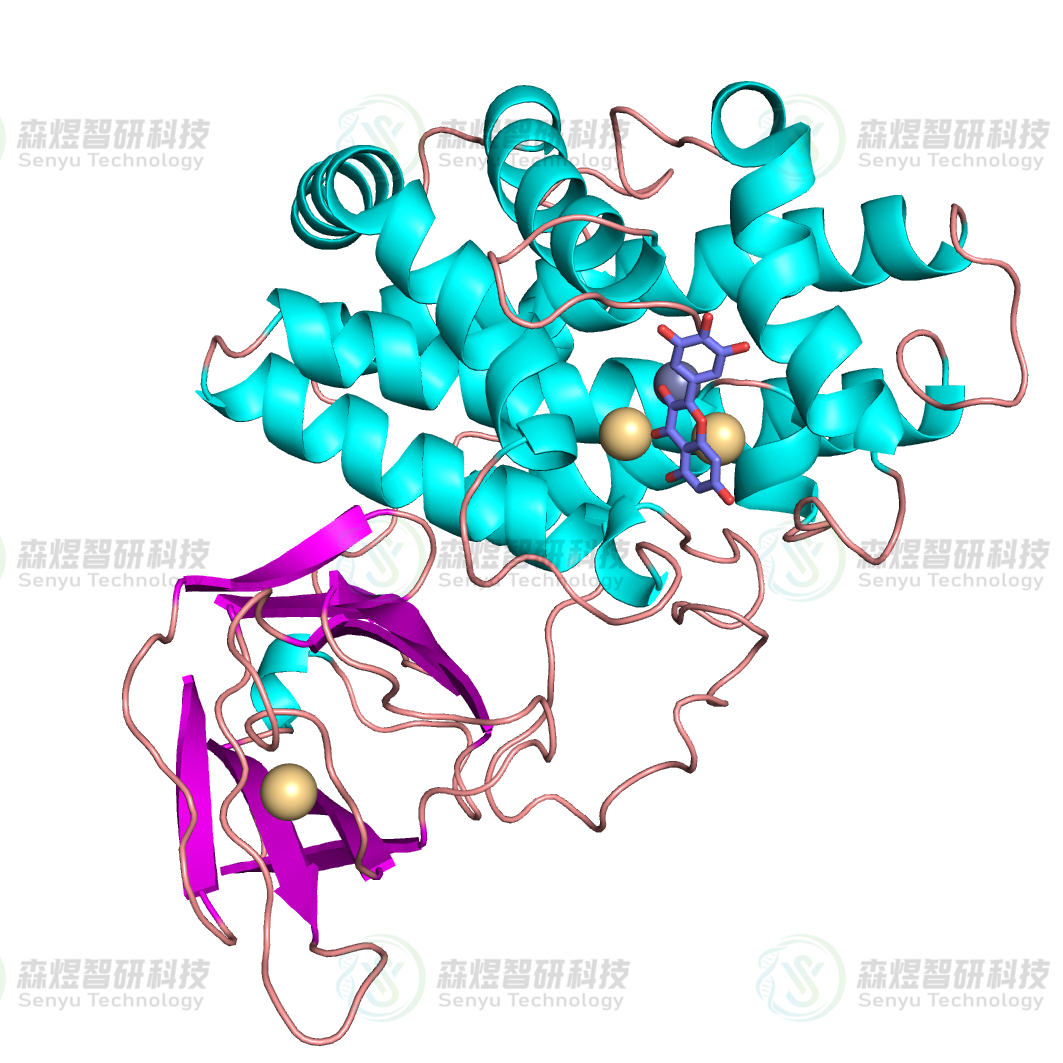
图5 CPA蛋白与MYR分子对接得到的复合物结构
3 模拟方法
3.1 分子动力学模拟
MD模拟采用Gromacs 2018.4程序[8],在恒温恒压以及周期性边界条件下进行。应用Amber14SB全原子力场[9],TIP3P水模型[10]。在MD模拟过程中,所有涉及氢原子的键采用LINCS算法[11]进行约束,积分步长为2 fs。静电相互作用采用(Particle-mesh Ewald)PME方法[12]计算。非键相互作用截断值设为10 Å,每10步更新一次。采用V-rescale [13]温度耦合方法控制模拟温度为298.15 K,采用Parrinello-Rahman方法[14]控制压力为1 bar。首先,采用最陡下降法对两个体系进行能量最小化,以消除原子间过近的接触;然后,在298.15 K条件下分别进行1 ns的NVT和NPT平衡模拟;最后,对体系进行50 ns的MD模拟,每10 ps保存一次构象,模拟结果可视化采用Gromacs内嵌程序和VMD完成。
4 结果与分析
4.1 MD模拟结果收敛性分析
均方根偏差(Root mean square deviation, RMSD)表示某一时刻的构象与目标构象所有原子偏差的加和,是衡量体系是否稳定的重要依据。本文将CPA蛋白与小分子MYR对接后形成的复合物体系命名为Complex(后面都以此缩写代替)。图6给出了Complex复合物中所有原子的RMSD随时间的变化,Complex整体的RMSD在模拟初期经历一个明显的上升,可能是此时复合物体系中蛋白刚与溶剂接触,与溶剂间相互作用较强,使其波动明显。随后在20 ns左右,此时体系的RMSD开始趋于稳定,稳定后的平均值为0.291±0.028 nm,表明基于该力场参数下动力学模拟是稳定可靠的,可用于后续的进一步深入分析。

图6 CPA蛋白与MYR复合物RMSD值随模拟时间的变化
4.2 RMSF分析
均方根涨落(Root mean square fluctuation, RMSF)可以表示蛋白质氨基酸残基的柔性大小,图7分析了整个体系中所有氨基酸的RMSF值。结果显示在Complex体系中CPA蛋白整体结构的RMSF值都较小,仅有S107-P119结构域的RMSF波动较大,表明整个CPA蛋白在模拟过程中结构并未发生明显解旋或变构。如图,对S107-P119结构域分析发现该区域是蛋白结构中一段柔性较大的Loop区,并且该段结构域离底物结合位点较远,不会对小分子化合物与蛋白间结合产生影响。整个CPA蛋白的RMSF整体波动值整体较小,并未因为MYR小分子的结合发生大幅波动,表明小分子与蛋白的结合是稳定的。
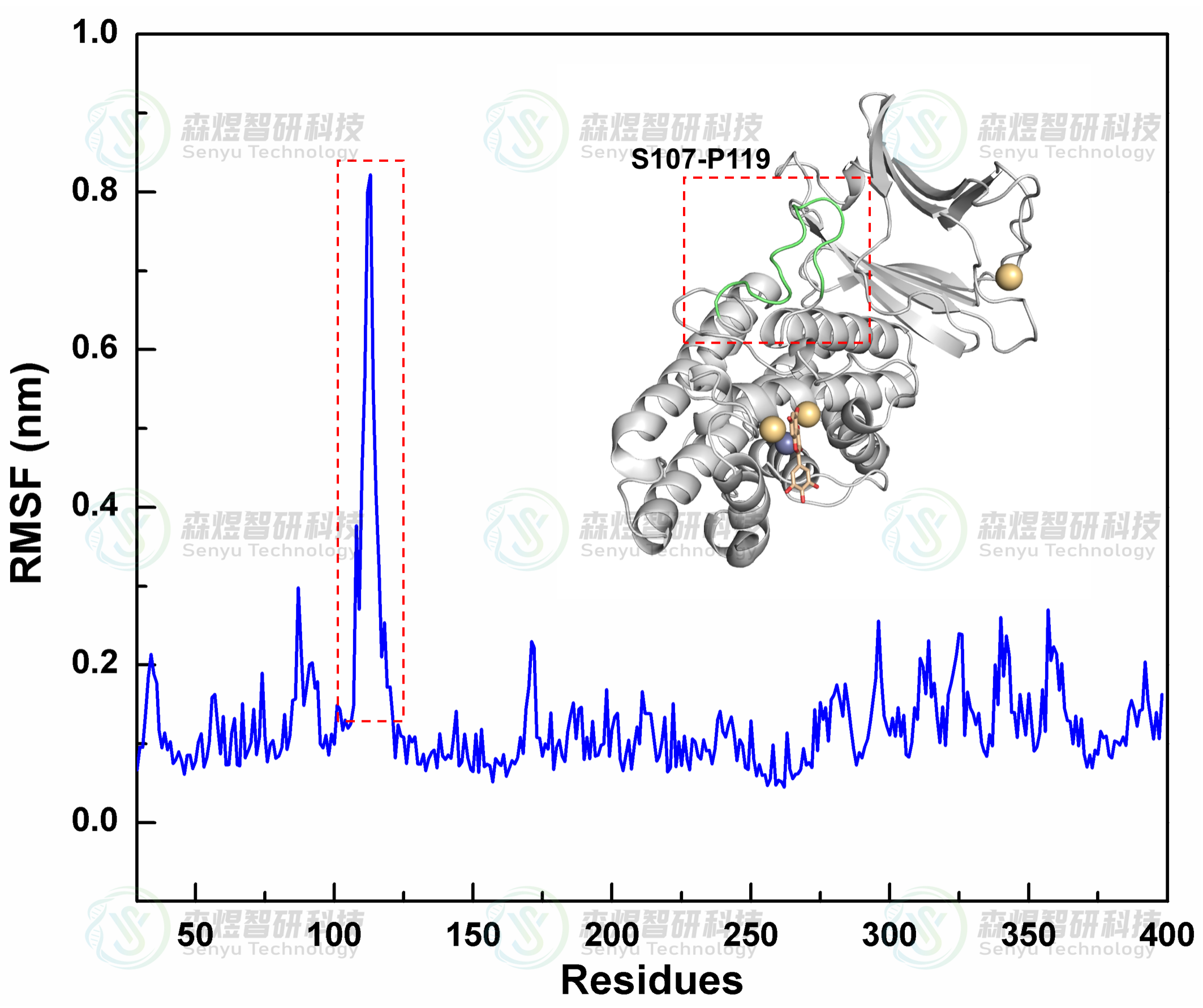
图7复合物体系中CPA蛋白氨基酸的RMSF分布
4.3 SASA分析
溶剂可及表面积(SASA)可以通过表征蛋白体系在溶剂环境中可被溶剂接触的分子表面积来分析模拟过程中蛋白在溶剂条件下的结构体积变化,SASA值越大表明蛋白结构更松散,体积也更大。为了研究复合物体系在模拟过程中的结构变化情况,本文对Complex复合物体系的SASA进行了分析,结果如图8所示。整个体系的SASA值在整个模拟过程中并未因底物的结合出现明显大幅波动,表明蛋白和MYR分子形成的复合物在溶剂体系中是非常稳定的,并未因小分子的结合导致整体蛋白结构出现明显的构象变化。
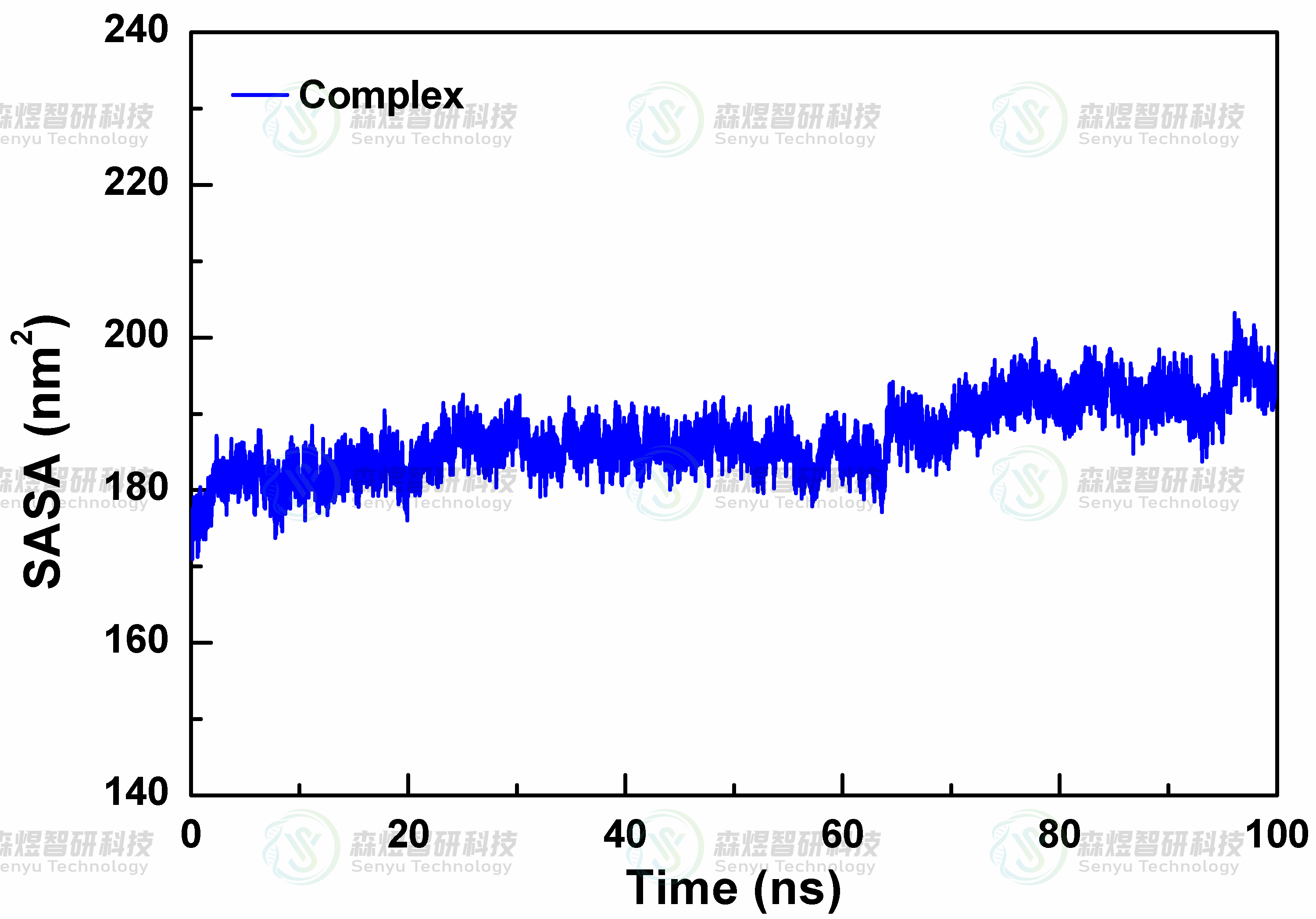
图8复合物体系SASA值随模拟时间的变化
4.4 MYR与CPA蛋白间的相互作用
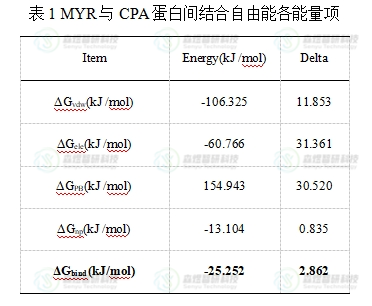
接下来,本文借助MM/PBSA方法计算了RMSD较为稳定的80-100 ns区间时CPA蛋白与MYR分子底物间的结合自由能,结果如表1所示,CPA与MYR间总的结合自由能为 -25.252 kcal/mol,其中体系的静电相互作用包括真空条件下的静电相互作用和极性溶剂化能(ΔGele+ΔGPB)为94.177 kcal/mol,对小分子和蛋白间的结合无明显促进作用;非极性作用可以作为疏水相互作用能,包括范德华力作用和非极性溶剂化自由能(ΔGvdw+ΔGnp),非极性相互作用为-119.429 kcal/mol,因此可以推断CPA蛋白与MYR分子的结合过程中,疏水相互作用能是主要的驱动力。
随后,为了进一步确认CPA蛋白与底物分子主要相互作用区域及哪些关键氨基酸参与了化合物与蛋白间的相互作用,本文提取MD模拟之后的复合物构象,对蛋白间的相互作用模式做了分析,结果如图9所示。从图9a和c中可以看出,MYR分子主要结合在CPA蛋白中Zn2+和Cd2+离子上方的疏水性空腔中,分子上整个占据了催化底物结合的空腔。从图9b和d中可以看出,MYR分子主要结合在由Trp29、Asp30、Gly31、Tyr93、Val177和Thr181氨基酸及Zn2+和Cd2+离子组成的空腔中,其中MYR分子环上的羟基与周围的Trp29、Asp30、Gly31、Val177和Thr181氨基酸间形成了较多的氢键作用,与Tyr93氨基酸间形成了疏水相互作用,同时MYR分子上的羰基O原子还与两个金属离子间产生了配位相互作用,进一步增强了MYR分子与CPA蛋白的亲和力。
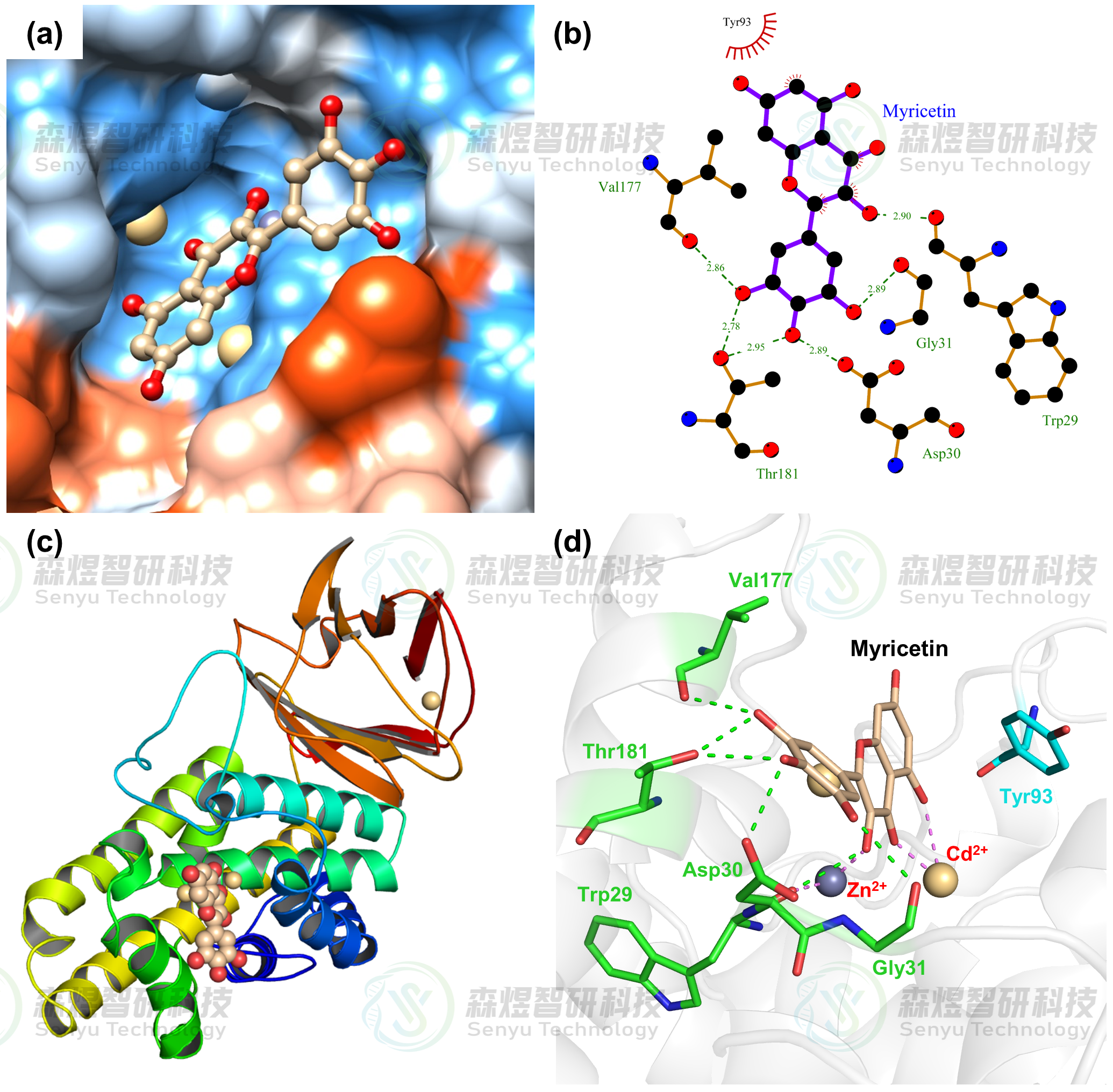
图9 MYR与CPA的结合模式图(a:MYR在CPA亲疏水性表面的结合,蓝色和橙色分别表示蛋白表面的疏水和亲水部分;b:MYR与CPA的二维结合模式,绿色虚线表示氢键作用,红色齿轮状表示疏水作用;c:MYR在CPA蛋白三维结构中的位置;d:MYR与CPA的三维结合模式图,绿色虚线表示氢键作用,紫色虚线表示配位作用)
5 结论
本文结合同源建模、分子对接和MD模拟方法研究了MYR分子与CPA蛋白间结合的稳定性及相互作用模式,通过100ns动力学分析发现,MYR与CPA蛋白结合较为稳定,并未导致蛋白整体结构大幅波动。通过MM/PBSA方法计算得到的结合自由能结果表明MYR在CPA蛋白口袋中主要通过氢键作用和非极性的疏水相互作用促进其稳定结合并与占据底物结合口袋,阻止底物与蛋白间的结合催化作用。本研究结果为MYR化合物与CPA蛋白的分子识别以及能否稳定结合并竞争性抑制该酶活性研究提供了理论指导。
参考文献
[1] Sansen S , Yano J K , Reynald R L , et al. Adaptations for the Oxidation of Polycyclic Aromatic Hydrocarbons Exhibited by the Structure of Human P450 1A2[J]. Journal of Biological Chemistry, 2007, 282(19):14348-14355.
[2] Waterhouse, A., Bertoni, M., Bienert, S., Studer, G., Tauriello, G., Gumienny, R., Heer, F.T., de Beer, T.A.P., Rempfer, C., Bordoli, L., Lepore, R., Schwede, T. SWISS-MODEL: homology modelling of protein structures and complexes. Nucleic Acids Res. 46(W1), W296-W303 (2018).
[3] Laskowski R A, Macarthur M W, Moss D S, et al. PROCHECK: a program to check the stereochemical quality of protein structures[M]. 1993.
[4] Sanner M F. Python: a programming language for software integration and development. J. Mol. Graph. Model., 1999, 17(1): 57-61.
[5] Stewart J J. MOPAC: a semiempirical molecular orbital program. J. Comput. Aid. Mol. Des., 1990, 4(1): 1-105.
[6] Stewart J J P. Optimization of parameters for semiempirical methods. III. Extension of PM3 to Be, Mg, Zn, Ga, Ge, As, Se, Cd, In, Sn, Sb, Te, Hg, Tl, Pb, and Bi. John Wiley & Sons Inc., 1991.
[7] Maier J A, Martinez C, Kasavajhala K, et al. ff14SB: Improving the accuracy of protein side chain and backbone parameters from ff99SB. Journal of Chemical Theory and Computation, 2015, 11(8): 3696-3713.
[8] Van d S D , Lindahl E , Hess B , et al. GROMACS: Fast, flexible, and free. Journal of Computational Chemistry, 2005, 26(16):1701-1718.
[9] Maier J A, Martinez C, Kasavajhala K, et al. ff14SB: Improving the accuracy of protein side chain and backbone parameters from ff99SB. Journal of Chemical Theory and Computation, 2015, 11(8): 3696-3713.
[10] Jorgensen W L , Chandrasekhar J , Madura J D , et al. Comparison of simple potential functions for simulating liquid water. Journal of Chemical Physics, 1983, 79(2):926-935.
[11] Hess B , Bekker H , Berendsen H J C , et al. LINCS: A linear constraint solver for molecular simulations. Journal of Chemical Theory & Computation, 1997, 4(1):1463–1472.
[12] Darden T A , York D M , Pedersen L G . Particle mesh Ewald-an N.log(N) method for Ewald sums in large systems. The Journal of Chemical Physics, 1992, 98:10089-10092.
[13] Berendsen H J C , Postma J P M , Van Gunsteren W F , et al. Molecular dynamics with coupling to an external bath. Journal of Chemical Physics, 1984, 81(8):3684-3690.
[14] R Martonák, Laio A , Parrinello M . Predicting Crystal Structures: The Parrinello-Rahman Method Revisited. Physical Review Letters, 2003, 90(7):075503.



